To derive individual tree light availability the light resources available to an individual (LRI), corrected for the overall light absoprtion at RU level, and the species-specific ability to utilize radiation are integrated to a measure of light utilization (f_light). f_light subsequently serves as weighting factor to calculate weighted leaf area (WLA), which in turn determines the individuals contribution to (or share on) APAR at RU level.

scaling LRI to resource unit level

LRI is aggregated bottom up based on individual tree light influence patterns. Its strength lies in an efficient approximation of an individuals' relative competitive status, while absolute levels of absorbed radiation are likely to be biased as an effect of the simplified computation. Actual radiation absorption is calculated at the RU level in iLand using Beers law. Although this is a somewhat erroneous approximation particularly for strongly structured stands, it is a robust and frequently applied method and alleviates the complexity of radiation interception modeling for individual tree crowns (cf. Brunner 1998, Lieffers et al. 1999, Duursma and Mäkelä 2007). Consequently, the bottom-up calculated LRI needs to be adjusted to achieve congruence with the RU level absorbed radiation (Eq. 1-3). This step constitutes a constraint on bottom-up LRI from a hierarchically higher level, in line with the hierarchical multiprocess scaling approach adopted in iLand. We follow Brunner and Nigh (2000) in defining an individual trees’ success to intercept radiation as a multiplier of PAR (Eq. 1), with WLA_j (m²) the weighted leaf area of individual j, a measure integrating both its leaf area and canopy status.

\[\begin{aligned} APAR=PAR\cdot SA\cdot pPAR=PAR\cdot \sum_{j}^{}WLA_{j} \end{aligned} \]

Eq. 1

Brunner and Nigh (2000) derive WLA_j as the integral over relative light availability and absorption for the crown volume of an individual (calculated by means of detailed ray tracing algorithms). In iLand, weight and contribution of every individuals' leaf area to RU APAR are approximated by a trees LRI_j (Eq.2).

\[\begin{aligned} WLA_{j}=LA_{j}\cdot LRI_{j} \end{aligned} \]

Eq. 2

Equating Eq. 1 and 2 a LRI correction factor is derived (Eq. 3), granting correspondence between RU level light absorption and individual tree LRIs:

\[\begin{aligned} LRI_{j}=LRI_{j}\cdot \frac{SA\cdot pPAR}{\sum_{j=1}^{n}LA_{j}\cdot LRI_{j}} \end{aligned} \]

Eq. 3

---

species-specific light utilization potential

Empirical results show that light utilization is not linearly related to absorption over species and light levels (Brunner and Nigh (2000)). Two light response curves- for shade-tolerant (S5) and shade-intolerant (S1) species- are used to confine the envelope of light utilization, following an approach frequently employed by gap models (e.g., Botkin 1993, Bugmann 1996, Seidl et al. 2005). Using LRI as input to these functions, the return value is interpolated applying the homogenized species shade tolerance ratings (s_tol) of Niinemets and Valladares (2006), Eq.4,

\[\begin{aligned} f_{light}=S1 + (S5-S1)\cdot\frac{s_{tol} - 1}{4} \end{aligned} \]

Eq. 4

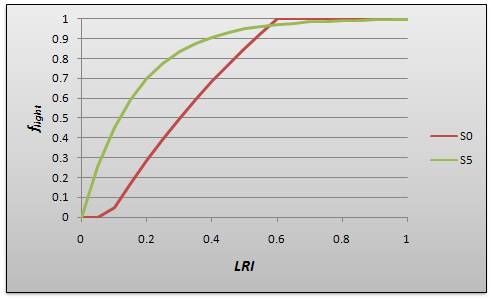Figure 1: Light response functions accounting for species-specific light utilization (S5= shade tolerant, S1= light-demanding)

---

individual tree radiation

The radiation available for primary production of individual j is derived as a share of total APAR using its LA_j and f_light,j as combined weighting factor (Eq.5)

\[\begin{aligned} APAR_{j}=APAR \cdot \frac{LA_{j}\cdot f_{light,j}}{\sum_{j}(LA_{j}\cdot f_{light,j})} \end{aligned} \]

Eq. 5

Due to the linear scaling of the applied radiation use efficiency approach the individual-tree weighting factor in Eq. 5, indicating relative competitive success of an individual in the resource unit, is identical for APAR and GPP.